Создание чертежей
 |
 |
 |
§
69. Определение истинной величины расстояний
Некоторые
задачи на определение расстояний рассматривались в предыдущих разделах. Например,
в § 42 определялась натуральная величина отрезка прямой линии методом треугольника,
в § 57 определялась натуральная величина отрезка способом плоскопараллельного
переноса. Эта задача может быть также решена способом замены плоскостей проекций
(см. § 58) или способом вращения (см. § 59). Определение длины отрезка
прямой позволяет решить задачу определения расстояния от точки до точки,
так как это расстояние и определяется отрезком прямой. Расстояние от точки
до прямой измеряется отрезком перпендикуляра, проведенного из точки к прямой.
Отрезок этого перпендикуляра изображается в натуральную величину на плоскости
в том случае, если он проведен к проецирующей прямой. Значит, нужно преобразовать
чертеж данной прямой, сделав ее в новой системе плоскостей проекций проецирующей
(см. § 58, задача 2). На рис. 140 определено расстояние от точки М до
прямой АВ:
1)
П2_|_П1-> П1_|_П4, П4 ||АВ,
П1/П4 ||A1B1;
2)
П1П4 -> П4_|_П5, П5
_|_AB, П4/П5 _|_A4B4;
3)
M5K5 — истинное расстояние от точки М до прямой
AB;
4)
чтобы построить проекции перпендикуляра МК в исходной системе плоскостей,
строят основание перпендикуляра— точку К—на прямой АВ из условия,
что в системе П4 _|_П5; он занимает положение линии уровня,
т. е.
M4K4_|_A4B4.
Горизонтальная и фронтальная проекции точки К определяются по линиям
из условия принадлежности ее прямой АВ. Расстояние от точки до плоскости
измеряется отрезком перпендикуляра, опущенного из точки на плоскость. Так как
перпендикуляр к проецирующей плоскости есть линия уровня, то удобно иметь на
чертеже «вырожденную» проекцию данной плоскости, т. е. преобразовать
чертеж (см. § 58, задача 3). На рис. 141 построены проекции перпендикуляра
МК, отрезок которого определяет расстояние от точки М до плоскости
Q(ABC):
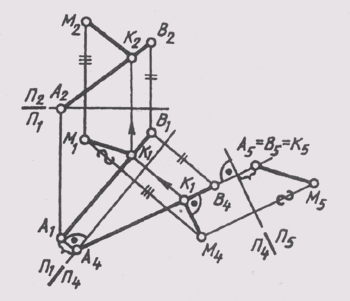
Рис.
140
1)
П1,П2->П1_|_П4, П4_|_Q,
П1 /П4 _|_ h(A, 1)~ 0;
2)
М4K4 _|_Q4 — истинная величина расстояний от
точки М до плоскости Q;
3)M1K1_|_K4Kl
или || П1/ П4;
4)
K2 построена с помощью высоты точки К, измеренной на
плоскости П4.
Расстояние
между параллельными прямыми измеряется отрезком перпендикуляра между ними. На
рис. 142 определено расстояние между прямыми а и b путем преобразования
чертежа прямых. Сначала построено
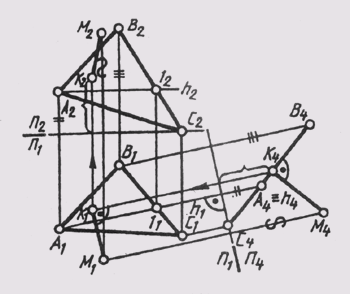
Рис.
141
изображение
прямых на плоскости П4_|_П1. В этой системе плоскостей
прямые занимают положение линии уровня:
а(b)||
П4; П1 /П4 ||а,(b1).
В
системе плоскостей П4 _|_ П5 прямые занимают проецирующее
по отношению к плоскости Пз положе-
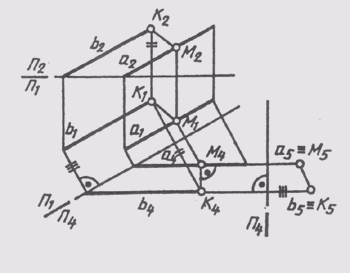
Рис.
142
ние:
П5 _|_ а(b); П4/П5 _|_a(b4)
Отрезок M5K5 между вырожденными проекциями прямых
определяет истинную величину расстояния между прямыми а и Ъ. Построения
проекций перпендикуляра МК в исходной системе плоскостей проекций аналогичны
рассмотренным ранее.
Для
определения расстояния между скрещивающимися прямыми необходимо одну из прямых
сделать проецирующей в новой системе плоскостей проекций.
Расстояние
от прямой до плоскости, параллельной прямой, измеряется отрезком перпендикуляра,
опущенного из любой точки прямой на плоскость. Значит, достаточно плоскость
общего положения преобразовать в положение проецирующей плоскости, взять на
прямой точку, и решение задачи будет сведено к определению расстояния от точки
до плоскости.
Расстояние
между параллельными плоскостями измеряется отрезком перпендикуляра между ними,
который легко строится, если плоскости займут проецирующее положение в новой
системе плоскостей проекции, т. е. опять используется третья исходная задача
преобразования чертежа.
 |
 |
 |
