Создание чертежей

 

§ 77. Прямоугольная изометрия

Прямоугольная изометрия характеризуется тем, что коэффициенты искажения составляют 0,82. Их получают из соотношения (1).

Для прямоугольной изометрии из соотношения (1) получаем:

Зu² = 2, или и = v - w = (2/3)^1/2 = 0,82, т. е. отрезок координатной оси

длиной 100 мм в прямоугольной изометрии изобразится отрезком аксонометрической оси длиной 82 мм. При практических построениях пользоваться такими коэффициентами искажения не совсем удобно, поэтому ГОСТ 2.317—69 рекомендует пользоваться приведенными коэффициентами искажения:

и = v = w — 1.

Построенное таким образом изображение будет больше самого предмета в 1,22 раза, т. е. масштаб изображения в прямоугольной изометрии будет М^А 1,22: 1.

Аксонометрические оси в прямоугольной изометрии располагаются под углом 120° друг к другу (рис. 157). Изображение окружности в аксонометрии представляет интерес, особен-

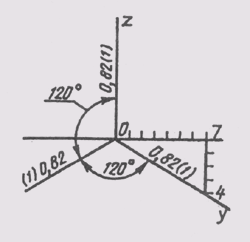
Рис. 157

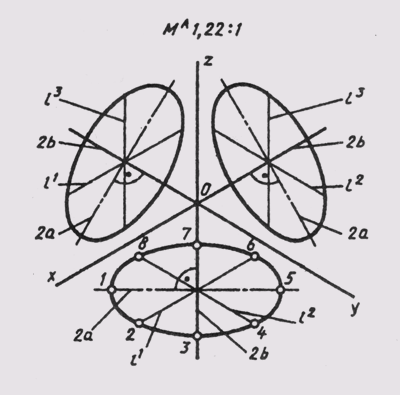
Рис. 158

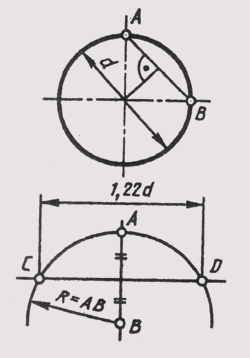
Рис. 159

но окружностей, принадлежащих координатным или им параллельным плоскостям.

В общем случае окружность проецируется в эллипс, если плоскость окружности расположена под углом к плоскости проекции (см. § 43). Следовательно, аксонометрией окружности будет эллипс. Для построения прямоугольной аксонометрии окружностей, лежащих в координатных или им параллельных плоскостях, руководствуются правилом: большая ось эллипса перпендикулярна аксонометрии той координатной оси, которая отсутствует в плоскости окружности.

В прямоугольной изометрии равные окружности, расположенные в координатных плоскостях, проецируются в равные эллипсы (рис. 158).

Размеры осей эллипсов при использовании приведенных коэффициентов искажения равны: большая ось 2а= 1,22d, малая ось 2b = 0,71d, где d — диаметр изображаемой окружности.

Диаметры окружностей, параллельных координатным осям, проецируются отрезками, параллельными изометрическим осям, и изображаются равными диаметру окружности: l¹=l² =l³ = d, при этом

l¹||x; l²||y; l³||z.

Эллипс, как изометрию окружности, можно построить по восьми точкам, ограничивающим его большую и малую оси и проекции диаметров, параллельных координатным осям.

В практике инженерной графики эллипс, являющийся изометрией окружности, лежащей в координатной или ей параллельной плоскости, можно заменить четырехцентровым овалом, имеющим такие же

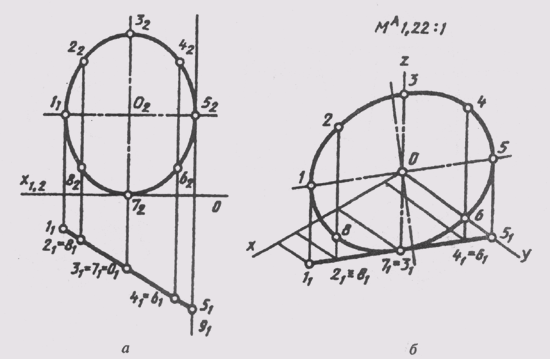
Рис. 160

оси: 2a = 1,22d и 2b = 0,71 d. На рис. 159 показано построение осей такого овала для изометрии окружности диаметра d.

Для построения аксонометрии окружности, расположенной в проецирующей плоскости или плоскости общего положения, нужно выделить на окружности некоторое число точек, построить аксонометрию этих точек и соединить их плавной кривой; получим искомый эллипс— аксонометрию окружности (рис. 160).

На окружности, расположенной в горизонтально проецирующей плоскости, взято 8 точек (1,2,... 8). Сама окружность отнесена к натуральной системе координат (рис. 160, а).Проводим оси эллипса прямоугольной изометрии и, используя приведенные коэффициенты искажения, строим вторичную проекцию окружности 1¹ ₁,..., 5¹₁ по координатам х и у (рис. 160, б). Достраивая аксонометрические координатные ломаные для каждой из восьми точек, получаем их изометрию (1¹, 2¹, ... 8¹). Соединяем плавной кривой изометрические проекции всех точек и получаем изометрию заданной окружности.

Изображение геометрических поверхностей в прямоугольной изометрии рассмотрим на примере построения стандартной прямоугольной изометрии усеченного прямого кругового конуса (рис. 161).

На комплексном чертеже изображен конус вращения, усеченный горизонтальной плоскостью уровня, расположенной на высоте z от нижнего основания, и профильной плоскостью уровня, дающей в се-

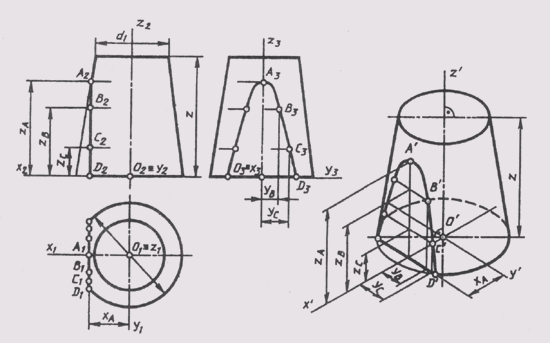
Рис. 161

чении на поверхности конуса гиперболу с вершиной в точке А. Проекции гиперболы построены по отдельным ее точкам.

Отнесем конус к натуральной системе координат Oxyz. Построим проекции натуральных осей на комплексном чертеже и отдельно их изометрическую проекцию. Построение изометрии начинаем с построения эллипсов верхнего и нижнего оснований, которые являются изометрическими проекциями окружностей оснований. Малые оси эллипсов совпадают с направлением изометрической оси О_Z (см. рис. 158). Большие оси эллипсов перпендикулярны малым. Величины эллипсов осей определяются в зависимости от величины диаметра окружности (d — нижнего основания и d₁ — верхнего основания). Затем строят изометрию сечения конической поверхности профильной плоскости уровня, которая пересекает основание по прямой, отстоящей от начала координат на величину X_A и параллельной оси О_у.

Изометрия точек гиперболы строится по координатам, замеряемым на комплексном чертеже, и откладываем без изменения вдоль соответствующих изометрических осей, так как приведенные коэффициенты искажения и = v = w = 1. Изометрические проекции точек гиперболы соединяем плавной кривой. Построение изображения конуса заканчивается проведением очерковых образующих касательной к эллипсам оснований. Невидимая часть эллипса нижнего основания проводится штриховой линией.