Создание чертежей

 

§ 43. Кривые линии

Кривые линии на комплексном чертеже задают своими проекциями, которые строят по проекциям отдельных точек, принадлежащих этой линии. Проекции линий при ортогональном проецировании получают как результат пересечения проецирующих цилиндров с плоскостями проекций (см. § 28); это означает, что проекциями плоских и пространственных кривых линий являются линии плоские. На рис. 79 видно, что секущая т кривой а в общем случае проецируется секущей ее проекции, а касательная/к кривой проецируется касательной к ее проекции.

На комплексном чертеже кривой ее особые точки, к которым относятся точки перегиба, возврата, излома, узловые точки, являются особыми точками и на ее проекции. Это объясняется тем, что особые точки кривых связаны с касательными в этих точках.

Если плоскость кривой занимает проецирующее положение (рис. 80, а), то одна проекция этой кривой имеет форму прямой. У пространственной кривой все ее проекции — кривые линии (рис. 80, б).

Чтобы установить по чертежу, какая задана кривая (плоская или пространственная), необходимо выяснить, принадлежат ли все точки кривой одной плоскости. Заданная на рис. 80, б кривая является пространственной, так как точка D кривой не принадлежит плоскости, определяемой тремя другими точками А, В и Е этой кривой.

Построение и изображение кривых рассматривалось в § 21,22, поэтому приведем пример изображения на чертеже только окружности как плоской кривой и винтовой линии как пространственной кривой.

Окружность — плоская кривая второго порядка, ортогональная проекция которой может быть окружностью и эллипсом (рис. 81, а). Для изображения окружности диаметра d на комплексном чертеже обязательно строят проекции центра О и двух ее диаметров. Удобнее всего строить проекции диаметров, параллельных плоскостям проекций: АВ || П₁ CD || П₂; CD _|_ П₁ (рис. 81, б). Фронтальная проекция окружности — эллипс — определяется малой осью эллипса A₁B₂ = dcos b и большой осью эллипса С₂D₂=d

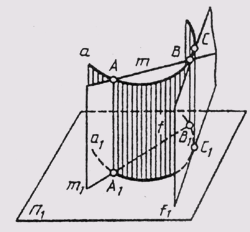
Рис. 79

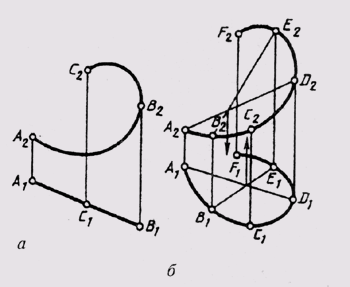
Рис. 80

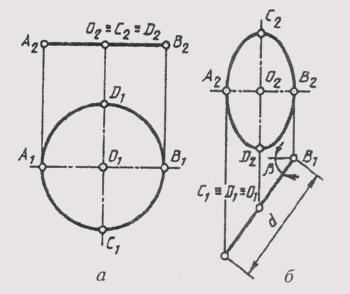
Рис. 81

Если плоскость окружности наклонена ко всем основным плоскостям проекций, то все три ее проекции есть эллипсы, которые можно построить по сопряженным диаметрам, являющимся проекциями тех диаметров окружности, которые параллельны плоскостям проекций (см. рис. 37).

Цилиндрическая винтовая линия (гелиса) — пространственная кривая, представляющая собой траекторию точки, выполняющей винтовое движение. Винтовое движение включает в себя равномерное поступательное движение точки по прямой и равномерное вращательное движение этой прямой с точкой вокруг оси i, которой прямая параллельна. Высота p, на которую точка поднимается по прямой за полный оборот, называется шагом винтовой линии (рис. 82). Если ось i винтовой линии перпендикулярна горизонтальной плоскости проекций, то горизонтальная проекция винтовой линии есть окружность, а фронтальная — синусоида.

Для построения фронтальной проекции винтовой линии при заданном диаметре d и шаге р нужно разделить и окружность, и шаг на равное число частей. Построение проекций точки винтовой линии показано на рис. 82. Цилиндрическую винтовую линию можно развер-

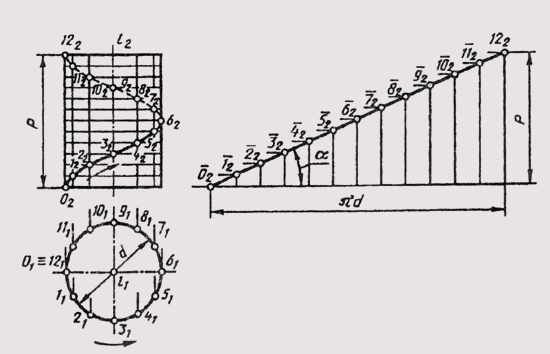
Рис. 82

нуть на плоскость. Развертка ее представляет собой прямую линию с углом подъема а, где tga = P / лd.