Создание чертежей

 

§ 52. Гранные поверхности

К гранным относятся поверхности, образованные перемещением прямолинейной образующей l по ломаной направляющей m. При этом если одна точка S образующей неподвижна, создается пирамидальная поверхность (рис. 97), если образующая при перемещении параллельна заданному направлению S, то создается призматическая поверхность (рис. 98).

Элементами гранных поверхностей являются: вершина S (у призматической поверхности она находится в бесконечности), грань (часть плоскости, ограниченная одним участком направляющей m и крайни-

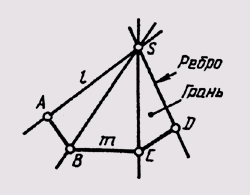
Рис. 97

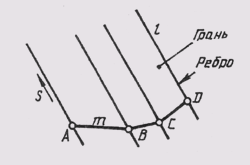
Рис. 98

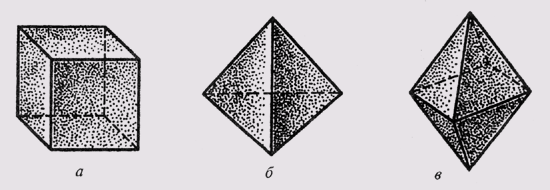
Рис. 99

ми относительно него положениями образующей l ) и ребро (линия пересечения смежных граней).

Определитель пирамидальной поверхности включает в себя вершину S, через которую проходят образующие и направляющие: l' ~ S;

l ^ т.

Определитель призматической поверхности, кроме направляющей т, содержит направление S, которому параллельны все образующие l поверхности: l||S; l^ т.

Замкнутые гранные поверхности, образованные некоторым числом (не менее четырех) граней, называются многогранниками. Из числа многогранников выделяют группу правильных многогранников, у которых все грани правильные и конгруэнтные многоугольники, а многогранные углы при вершинах выпуклые и содержат одинаковое число граней. Например: гексаэдр — куб (рис. 99, а), тетраэдр — правильный четырехугольник (рис. 99, 6) октаэдр — многогранник (рис. 99, в). Форму различных многогранников имеют кристаллы.

Пирамида — многогранник, в основании которого лежит произвольный многоугольник, а боковые грани — треугольники с общей вершиной S.

На комплексном чертеже пирамида задается проекциями ее вершин и ребер с учетом их видимости. Видимость ребра определяется с помощью конкурирующих точек (рис. 100).

Призма — многогранник, у которого основание — два одинаковых и взаимно параллельных многоугольника, а боковые грани — параллелограммы. Если ребра призмы перпендикулярны плоскости основания, такую призму называют прямой. Если у призмы ребра перпендикулярны какой-либо плоскости проекций, то боковую поверхность ее называют проецирующей. На рис. 101 дан комплексный чертеж прямой четырехугольной призмы с горизонтально проецирующей поверхностью.

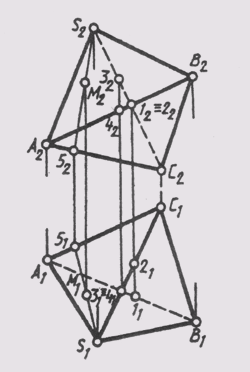
Рис. 100

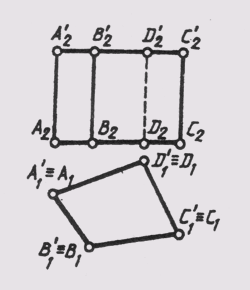
Рис. 101

При работе с комплексным чертежом многогранника приходится строить на его поверхности линии, а так как линия есть совокупность точек, то необходимо уметь строить точки на поверхности.

Любую точку на гранной поверхности можно построить с помощью образующей, проходящей через эту точку. На рис. 100 в грани ACS построена точка М с помощью образующей S-5.